atcoder_drills4

ABC126以降（6問構成）の E/F 埋めていこうかな (2021-04-23 memo)。

ニブタンで TLE, ニブタン＋累積和で AC: 27579333

201 通り検討すれば、そのなかで、mod 200 で分類したときに同じになるものが必ずある！なるほど！

わかんなくて、解説みた。

まず、\(0 \oplus 1 \oplus 2 \cdots \oplus (2^M - 1)\) が 0 になること（排他的論理和が \(2^M -1\) になるペアを偶数個つくれるので）に気づく（または知っている）必要があった。

また、そのことから、K 以外の 0 以上 \(2^M - 1\) 以下の整数すべての数の排他的論理和は、 \((0 \oplus 1 \oplus 2 \cdots \oplus (2^M - 1)) \oplus K\) となり、前半の括弧でくくった部分が 0 であることから、式全体の値は K になります。

以上のことがわかっていれば（加えて、若干の慣れがいるとは思うけど）、解説にあるようなこたえが思いつけるかなぁ： 21964825

とけたけど、直前の桁の状態のみ用いる桁 dp だったので、状態変数を配列にする必要はなかった： 21630951

方針がたってから、AC までに随分てこずってしまった。

入力の数列を、非負の要素と負の要素にわけて、それぞれ絶対値の大きいものから順にならべる
答えが正になると仮定すると、以下の手順で答えがつくれる
- 非負の要素、負の要素、それぞれの先頭二つの積を比較する
- 非負の方が大きければ、非負の要素をひとつ取り出して用いる（ここがキモ）
- 負の方が大きければ、負の要素を２つ取り出して用いる
答えが正にできないときには、全要素を絶対値でソートしたものの小さいものから k 個かけたものが答え

ひっかかったのは、以下の３点：

正の要素はひとつずつ用いる（上述の「キモ」の部分）
先頭２要素を書けたものは、long long に収まるのでそのまま大小比較するのだが、それと答えを求める変数をそのまま掛けると桁あふれしてしまう。（mod をとってからかける）
負になるケースは、絶対値でソートしたものを用いて単純に書いた方がいい

提出例：21588624

これを落としたのは痛かった。反省。

値の小さい色から取っていくのだけど、ある色 Ci を塗り終わった時点の状態としてありうるのは、同じ色 Ci のうち一番右端のものの位置にいるか、一番左橋のものの位置にいるかの二通り。

そこで、以下のような状態を更新する dp を考える：

実際には、dpx[i+1] を求めるのに、ひとつまえの dpx[i] しか必要としないので、状態を配列でもつ必要はない。

あとは、存在しない色の処理に少し気を付ける： 21374425

2-SAT は、蟻本 p.288～にあるように SCC を用いて解くことができる。また、ACL にはずばり 2-SAT を解くライブラリもある。

SCC を使った投稿例：21269641
2-SAT を使った投稿例：21269316

この問題では、N ≦ 1000 なので (i, j) の全組み合わせについて距離が D 未満かどうかチェックして辺を張ることができたが、ARC069F - Flags では N ≦ 10000 なので同じようにはいかなくて難しい（D について二分探索すればいいのだけど、辺を張るのに同じやり方では TLE になるはず）。

わかんなくて、解説みて実装。実装はむずかしくない： 21248311

min, max の合成がうまくできずに敗退。以下の 4 つを使えるようにしておこう。

max(x, y) + z = max(x+z, y+z)
min(x, y) + z = min(x+z, y+z)
max(x, min(y, z)) = min(max(x,y), max(x,z))
min(x, max(y, z)) = max(min(x,y), min(x,z))

2 も同様に示せる。

3, 4 は、x, y, z の大小関係６通りそれぞれについて値を書き出して、同じになることを確認してしまおう。

**表 1:** max(x, min(y, z)) = min(max(x,y), max(y,z))
x, y, z の大小関係	max(x, min(y,z))	min(max(x,y), max(x, z))
x ≧ y ≧ z	x	x
x ≧ y ≧ z	x	x
y ≧ z ≧ x	z	z
y ≧ x ≧ z	x	x
z ≧ x ≧ y	x	x
z ≧ y ≧ x	y	y

**表 2:** min(x, max(y, z)) = max(min(x,y), min(y,z))
x, y, z の大小関係	min(x, max(y,z))	max(min(x,y), min(x, z))
x ≧ y ≧ z	y	y
x ≧ y ≧ z	z	z
y ≧ z ≧ x	x	x
y ≧ x ≧ z	x	x
z ≧ x ≧ y	x	x
z ≧ y ≧ x	x	x

これらを使うと（４番目は使わないけど）、以下の通り \(f_i (x) = \min (c, \max(b, x + a))\) の形で表される関数の合成を求めることができる：

\(f(x) = \min(c_1,\max(b_1,x+a_1))\)
\(g(x) = \min(c_2,\max(b_2,x+a_2))\)

\[ \begin{align*} g\circ f(x) &= \min(c_2, \max(b_2, f(x)+a_2))\\ &=\min(c_2,\max(b_2,\min(c_1,\max(b_1,x+a_1))+a_2))\\ &=\min(c_2,\max(b_2,\min(c_1+a_2,\max(b_1+a_2,x+a_1+a_2))))\\ &= \min(c_2,\min(\max(b_2,c_1+a_2),\max(b_2,b_1+a_2,x+a_1+a_2)))\\ &=\min(c_2,\max(b_2,c_1+a_2),\max(b_2,b_1+a_2,x+a_1+a_2))\\ \end{align*} \]

となり、\(c = \min(c_2, \max(b_2,c_1+a_2))\), \(b = \max(b_2, b_1+a_2)\), \(a = a_1+a_2\) とすると、 \(g\circ f(x) = \min(c,\max(b,x+a))\) となる。

提出コード： 21175458

解説読んでもいまいちわからず、解説動画をみてようやくなっとく。

升目に数字をうめたけっか、A={Ai} (i = 1, ..., N) と B={Bj} (j = 1 ,..., M) が定まるわけなのだが、この問題を解く上では、「A, B がどのような条件を満たせば、それを実現するような升目の埋め方が存在するか」を考えて、その条件を満たすような A, B を数え上げるというように、定義とは逆の順序で考える感じ。

それがわかれば、あとは、比較的理解しやすいかと思う。

N = 1 のときには、B が決まれば A は自動的に決まってしまうのだが、B の自由度には制限がないので \(K^M\) 通り
M = 1 のときも同様に考えて \(K^N\) 通り
\(K,\ M \ge 2\) のときには、max(A) <= min(B) を満たすものを全て数え上げればいい

最後のものに関しては、max(A) = x (x = 1, 2, ..., K) の各ケースについて数え上げればよくて、\(\Sigma (x^N\ - \ (x-1)^N) \ \times \ (K - x + 1)^M\) となる： 20843039

row, col を取り違えていちど WA だしてしまった： 20813606

なるほどねぇ、という感じ： 20790435

復習。原理的なところは覚えていて書けたのだけど TLE。累積和を用いた dp にしないと時間がおさまらないんだった： 20791455

LCS を覚えていたせいで、早とちりして間違えた。２つの文字列の LCS の長さをもとめて（それを lcs とする）、max(n, m) - lcs が答えとしてしまった。「入力例」はたまたまそれで合うが、たとえば、次のような入力で間違う：

LCS は 1 2 3 なので、7 - 3 = 4 と答えてしまうが、正しくは 5 なので。

LCS を求めるのを似た dp で正しいこたえが出せるので、LCS を知っていることは有利にはなるのだけど、こういう早とちりはよくない： 20756687

復習だったが、書けず。

ひとつ前の状態のみから次が決まるので、配列でなくてもよいタイプの dp
a + b < L が確定している場合とそうでない場合で状態を２つもつ (dp1, dp0)
着目している桁が 0 のとき
- dp0 側は (a, b) == (0, 0) しかだめなので、t0 = dp0
- dp1 側はなんでもよい((1, 0), (0, 1), (0, 0)) ので、t1 = dp1 * 3
- 0/1 の行き来はなし
着目している桁が 1 のとき
- dp0 は、a+b = 1 になる組み合わせの場合 ((1,0), (0,1)) に 0 側にとどまるので t0 = dp0 * 2
- dp1 は、0 側からこちらに遷移するケースもあるので t1 = dp0 + dp1 * 3
(mod p) わすれずに

提出例： 20686063

参考：ARMERIA: AtCoder Library Practice Contest I - Number of Substrings

提出コード：20660818

参考：kmjp'2 blog: square869120Contest #2 E - 部分文字列

提出コード： 20660944

葉をノードにみたてた最大流問題。ポイントが２つある。

各ノードを in と out にわけ、in から out に容量 1 の辺を張る
同一行または同一列にあるノード同士を容量 INF の辺で互いに結ぶのだが、文字通りにやると、辺の数が多くなりすぎる → 各行、列に「スーパーノード」を用意し、各ノードはスーパーノードとの容量 INF の辺をもつ（行きと帰り）

提出コード： 20662346

時間をおいて復習。最初の桁に対して 0 を選ぶ際には「使える数字」を消費しないというのは覚えていて対応できたのだけど、WA を繰り返してしまった。 dp 配列は、dp[i][bm] の二次元じゃなくて、もう一次元加えて正の場合と負の場合を別々の状態としてもたないといけなかった。なんでそうしないといけないのか、腹に落ちてないから間違うんだな： 20667025

差が正のときと負のときとで、とるべき戦略が違うので、両者の状態が縮退していてはいけないというのは、なんとなくわかるけど…

Longest Common Subsequence に関する基本問題。しらべつつ書いた： 20667920

直前に上述の LCS を解いてたのででけた。こんどは自力ですらすらと書けたかな： 20669881

いっぱつ、入力が一文字だったケースの処理をぬかしてて WA.

復習なので、方針はすぐに立ったのだけど、なんどもバグって前回の AC プログラムを確認したりした。まだ自力で解けてない感： 20672771

二部マッチング問題を最大流問題へ帰着してとくやつ。なんども WA だしてしまったけど、flow をもとめたあとにマッチングしている経路としていない経路を見分けるのに edge.flow をみるべきだったという： 20650078

MinCostFlow は流量を最大にしようとするので、入力例２のケースのようにあえて K 個選ばない方がいいケースをどう対処するのかが難しかった： 20654290

各辺の「コスト」は flow 1 あたりのコストなのよね。

最小カットをつかって「埋める燃やす」問題を解く」もみよ。

条件は K(K+1) が 2N の倍数であることと言い換えられる。そこで、2N を xy = 2N を満たすように因数分解して、K が x の倍数で (K+1) が y の倍数になるような K のうち最小のものを答えればよい。

x は 2N の約数を全部列挙、それぞれに対して y = 2N / x とする。

\(K \ \equiv \ 0 \ (\textrm{mod} \ x)\)
\(K \ \equiv \ -1 \ (\textrm{mod} \ y)\)

の両方を満たす正の整数 K を求めたいのだが、これには crt が使える: 20577126

異なる部分だけとりだして、その部分が３回以内のスワップで一致させられるかを調べ云々という筋道は解説どおりの方針をたてたのだけど、そのスワップ回数のカウントがわからなくなってしまった。（はじめ転倒数かなと思って実装したのだけど、当然、全然合わず。）３回以内で一致させられるかどうかの判定部分は、規模が小さいので全探索と。なるほど： 20513607

操作２は、一つ飛ばしの位置にある２つの要素を交換するので、この操作によって要素の位置（インデックス）のパリティがかわらない。そこで、元の数列での位置が奇数で、ソート後に偶数になるものの個数（これは、元が偶数でソート後奇数になるものの個数と等しい）を数える： 20491832

復習にかいめ。

とけた！…けど、随分てこずってしまった。解説にあるように、セグメントツリーを用いて求めたのだけど、一番左の列や最も上の行に岩がある場合の考慮がもれていて何度も WA を出してしまった： 20472839

確率 dp …… なんだけど、むずかしかった。

ゴール地点での期待値 0 を初期値として、ゴールまでの手数の期待値を後ろから求めていく。ただし、「振り出しに戻る」駒の期待値はスタート地点における期待値と同じなので、普通の確率 dp のように後ろから求めていくことができない。

そこだけ変数 X のようにしておいて、f(i) = aX + b の形で確率 dp していくと、 f(0) = X = AX + B が求まるので、最後に X = B / (1-A) として解けばいい。

…と、これだけでも難しかったのですが、確率 dp の部分も累積和をとりながらでないと TLE になる： 20466423

メモ化再帰、だが、選択肢を減らさずに常に +1, -1, x2 の全ての分岐をしていたら発散してしまう。

そこで、選択肢を減らすことを考えるのだが、x から y に近づけるのではなく、y から x にすることを考えると減らしやすい。二倍するのはいつでもできてしまうが、逆方向を考えると、二で割れるのは偶数のときだけなので。

なお、もう少し考える必要がある。Y から X に向かう最小手順は、以下のどれか：

+1 or -1 を | y - X | 回繰り返すことで到達する
奇数に +1 または -1 を施して偶数にする
偶数を何度か 2 で割ったあとに、+1 または -1 を必要なだけ施して x に到達する

偶数に二回 1 を足したり引いたりして、違う偶数にしてから２で割るようなことはしない。

また、奇数のうち 1 は「２で割る」の結果これになるので、また +1 して偶数にするようなこともしない。このあたり、解説もよんでもういちどよく考えよう。

なお、べつにこれ（Y から X への逆方向を考える）が唯一のやりかたというわけでもないらしい： 20435169

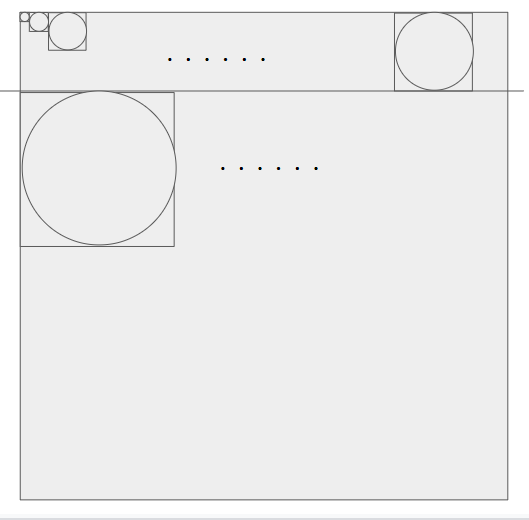
領域には余裕があって、割とどうやっても入る感じなので、小さいものから置いていった。縮尺てきとうだけど、下図のように円が正方形領域を占めるものとして（厳密に円同士の距離を考えたりしない）横につめていって、端までいったら（ぴったりにはならない）「次の列」へうつる：

提出コード： 20444530

解いたことがあるので、どうにか解けるといった感じ： 20409111

今日の水色： 20416993

復習…なのに、めちゃめちゃ苦戦した。

\(S + xK \equiv 0 \ (\textrm{mod} N)\) を満たす x を求めればいいのだけど、これを変形して \(xK + yN = N-S\) を満たす x を求める問題に帰着させる。

拡張ユークリッドの互除法により、\(xK + yN = \gcd(K, N)\) の解がもとまるので、この解をもちいて x * (N-S) / gcd(K, N) が答えとなる (x 回移動するたびに、gcd(K, N) 個となりに移動するので、x * (N-S) / gcd(K, N) 回移動すれば、最初の位置から N-S だけ移動して「玉座」にいける)。

ただし、以下に注意する必要がある：

(N-S) が gcd(K, N) の倍数でないときには解なし
拡張ユークリッドの互除法の結果においては、x が負になる場合があるので (x + N) % N を用いる
N / gcd(K, N) 回ごとに一周するため、これで割ったあまりを答え（最小解）とする

提出コード： 20426439

N 回 dp やるんだなとは思ったんだけど、コンテスト中は残り時間も少なくて書けなかったもの。今日考えてみたけど、やっぱり書けず。昨日の自分には書けなかったな、これは。要復習： 20369499

なんてことないんだけど、1457 を切り上げて 1460 にしてしまうようなミスで一度 WA:20370434

ニブタンいっぱつだーと喜んで submit して WA 連発するという（なんと 11 回）。基数がかなり大きな数になることがあるので、judge 関数のなかで long long すら溢れる場合があるというのと、一桁のときは基数を変えても数字がかわらんということへの対処の２点はまりどころがあって、どっちもはまっていた。あふれについては、__uint128_t をつかって回避（コンテスト中にも AC したが、あとで少し整理したものにリンクしておく）： 20351152

M 自体は long long に収まるのだから、溢れたら ng ってやれば __uint128_t に頼らなくてもいけるかなぁと思ったのだけど、1WA 残る。かなり多くの人が D 落としてしまったのは、これかな： 20350950

解説にはなんかむずかしいことが書いてあるが、以下の漸化式で DP できる（ @kyopro_friends さんのツイートの図も参照）。

引き算があるので、mod をとった結果が負になる場合の処理がいった： 20258607

tsugittaさんの解説が詳しい： 20258992

なんども WA を出した。線分と辺が交差する回数を数えるのだけど、与えられているのが直線ではなく「線分」なので、判定をもうすこし正確にする必要があった。

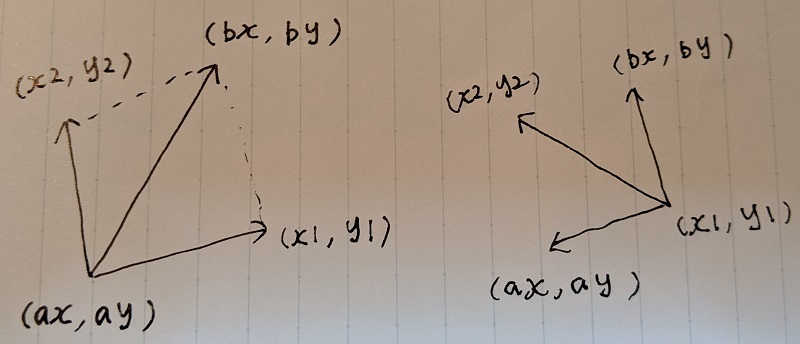
交差の判定は、ベクトルの外積を用いた「符号付き面積」で行うのがいい（線分が水平や垂直の場合もそのまま扱える）のだが、線分 A-B が短いために交差しないケースもあるので、上図の左の形での判定だけでなく、右の形でも判定して、いずれも OK の場合のみ「交差」となる： 20247064

ふつうにシミュレートできる。時系列のイベント queue として、priority_queue をつかった： 20248708

もういっかいやっておこう：20230054

とけた： 20231769

なかなか合わせられなかった。もういちど解いておこう： 20234229

※はまったポイントは提出コードのコメントに記載（二か所）

ひとつめに関しては、かならずループはあるのだから、ループ検出するまで繰り返せばよかった。

各教室の被覆数（何人がその教室を担当しているか）を Imos 法で求めるというのは思いついたのだけど、各担当者の範囲に被覆数１の教室を含むかどうかをすばやく判定する方法が思いつかなかった。

解説にあるとおり、被覆数が１であるような教室の場所が１、そうでない場所が０であるような配列の累積和を用いると、各区間に被覆数１であるような教室を含むかどうか（何個含むか）をすばやく求めることができる： 20204846

でけた： 20205550

どうも Min-Max 的探索を書いてしまって TLE しがち。メモ化していて計算量は同じかなぁと思ったのだけど。もっとシンプルに Judge を一本化できる： 20191654

だいたいこんな感じかなぁと思ったものの、つめきれず。のちほど再挑戦。プログラム自体は簡単： 20193097

DP と思って眺めてたのに書けなかった。要復習！

入力１に関しては、下記のような dp 配列になって、これを全部足したものが答え。メモ化で素直に書ける：20181763

※ typo でバグったりもした。要注意。

重み付き座標の重心のようなものを求めるんだろうか…とか考えてたどり着けず。そうかぁ、ニブタンかぁ。そうだなぁ： 20141178

難しそうと思ってしまった。

非負整数の列から累積和をつくれば non-decreasing になるなぁと気づけば、

すべてゼロ以下の数列からも同様に累積和をつくる要領で Non-decreasing にできる
一般の数列も N 回以下の操作で、ゼロ以上もしくはゼロ以下ばかりの数列にできる

というので、かならず 2N 回以下で可能： 20141653

普通に書くだけだったのだけど、ちょっとバグって時間がかかった（タイポ的ミスだった）のと、コーナーケース（first = last の場合や、到達不可だった場合）処理がぬけているのを入力例２，３に救われたりしたのは要反省： 20116524

なん日か前にわからず解説みて、少し寝かせてあったやつ。どうにか AC のプログラムは提出したが、なんかあやふや： 20123174

解説を素直に実装すると、こんな感じになりそうに思えるんだけど、これだと WA なんですよね。同じ方法であれこれ実装しても、おなじく WA となるので、実装上のミスというより方法にあやまりがあるようなのだけど…。

ひとまず、体重の軽いものから正しい荷物を持たせればいいという方法のコードを提出した。解説にある考察に関して要復習： 20092744

桁 dp と Bit dp の組み合わせ。かけた！…んだけど、AC でるまで何度も間違えた。

電卓の場合、押さなきゃいいだけなので、最初の桁を 0 にするのは数字を使ったことにならない
差が正で推移する場合と、負で推移する場合と別にもつ。（ただし、０から正、負への遷移があるので両者を完全に別系統とは扱えない）

提出コード： 20108362

出題意図とは違うやり方で解けてしまった…のだけど、int あふれて一度 WA だしてしまった： 20109994

あとで、解説にある方法もみておこう。

単調増加ではないけれど、連続、かつ、初期値が f(0) < 100, f(200) > 200 が示せるのでニブタンで求まる。また、こういった浮動小数点数ニブタンでは ok と ng の差で while ループにするのでなく、固定で 100 回とか回せばよい： 20112064

解けた、が、未使用アルファベットの扱いをさぼって最初 WA だしてしまった。はじめから単純にやればよかった： 20084371

とけた。が、入力２がなかったら（４つ焼くより３つ焼いたほうがいいケース）WA だしてたと思う： 20084696

bitDP。自力では解けなかったので要復習。

25ビットで、使用済の数字、または、すでに埋まっているマスを表現するのだろうなぁとは思ったのだけど、マスの埋まり状況と数字の使用状況、着目しているマスがどれで…みたいなことを状態に持とうとしたら、何次元配列になるのかしら…とか悩んでしまった。

解説にあるように、数字の１から順につかっていくことに決めると、マスの埋まり状況を表現するビットマップだけで、マスの状況と次に使う数字がわかる！（すでに埋まっているマスの個数＋１が次の数字なので）。

また、これも解説にある通りだが、１から数字をうめていくことにきめると、置けるケース、置けないケースの判定が単純にできる。

２５マスとも空の状態から、数字の１から順に置いていくので、入力であたえらえる情報は、すでに埋まっている数字と考えるのではなくて、そのマスにおける数字を制限していると考えればよい。

提出コードは、ほぼ解説のまんま（のつもり）： 20088881

二次元累積和。黒と白で符号を逆にしておけば、「たしてゼロ」が求める状態になる。 H, W <= 100 の制約で \(\textrm{O}((HW)^2)\) でいけるのね、というので少し迷った： 20064273

最終的には自力で通したのだけど、回り道をしてしまった。 N <= 12 なので全通り試せる： 20064900

入力文字列を二つにわける。あり得る分け方すべてについて、２つの文字列の最長共通部分列長を求めればよい： 20049411

最長共通部分列 (LCS; Longest Common Subsequence) については、 Educational DP Contest の F LCS で復習しておくのがいい。

以下の方針で与えられたパスワードを加工するプログラムを提出したのだが、WA

先頭文字が 'a' でない場合には、先頭文字をひとつ小さくし、さらに、
1. 後続文字列のなかに 'z' でないものがあったらそれをひとつ大きくする
2. 後続文字列がすべて 'z' だった場合には、文字列の後ろに 'a' とつけたす
後続文字列が 'a' の場合には、先頭を 'a' と取り除き、さらに、
1. 後続文字列のなかに 'z' でないものがあったらそれをひとつ大きくする
2. 後続文字列がすべて 'z' だった場合には、文字列の後ろに 'a' とつけたす

1の2のケースで、加工後の文字列の長さが 20 を超えてしまうケースの考慮が漏れてしまっていた： 20051382

復習。今回は、各連結成分が木か否かを判定するのに、各連結成分に含まれる辺の数を保持しておいてそれを用いるようにしてみた（前回は、DSF で判定しようとしてややてこずった）： 20052137

復習。方法はわかっていたのだけど、C++ で書くのがはじめてで、えらいはまった。

計算途中であふれることも多いので、int ではなく ll を使おう
ニブタンの (ng, ok] は開区間なので、ng の初期値は 0 ではなく -1
いろいろやり直す過程で 1 << 60 とかやって嵌る（1LL << 60 でないとだめ）

など。どれもあるあるなのだけど、見直しておいてよかったかな： 19950214

解けた…が、ちゃんと証明せずに半信半疑で提出してしまったので、そのあたり要復習： 19929241

ふつうに全探索： 19929510

復習。めぐる式： 19932295

とけた： 19917722

とけた： 19918292

いっぱつ WA を出してしまった。どこにも石がないケース。

解けた、けど、ちょっと書くのにてこずりすぎ： 19890766

Rate に関する累積和と、（レート、手）を出した人の人数をカウントしておくことで計算可能。

…なのに、うまく比較関数を書いてやればソートできるかなぁと考えてしまって答えが合わなくて嵌った。二者を正しく大小比較はできるけど、じゃんけんなので全体の順序は決められないんですよね。そりゃそうだ： 19867365

N <= 1000 なので Warshall-Floyd でいけた…のだが、 corner-case と名のついたテストケースで WA。なかなか何故かわからなかった。 dp[s][k] == dp[k][t] となるケースには、k が中継点として適切な場合以外に、 k に到達できない場合 (dp[s][k] == dp[k][t] == INF) が含まれていた： 19879315

もうちょっと N が大きい場合には、s, t それぞれを始点とした dijkstra をやるのだろう。そっちも確認しておこう。

Dijkstra 版。たしかに、だいぶ速い： 19883895

文脈自由文法は括弧の対応を数えられるのだ的な。自力でといたけど、二回 WA を出してしまった。 "{X}" が set になる（１要素のときはカンマが出現しない）ことに対応する部分で： 19848414

下に凸であるような関数なので、３分探索 (Ternary Search) できる。

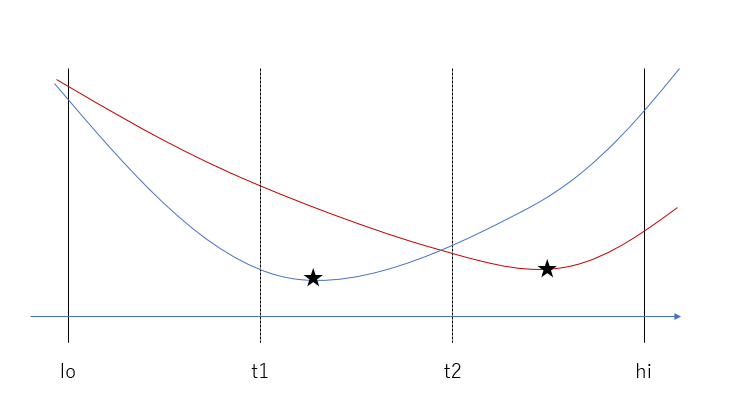
f(t1) >= f(t2) の場合（上図の赤線のような形）には、次の探索範囲を [t1, hi] に、そうでない場合には [lo, t2] にする： 19852531

惨敗した ABC186D の復習。この D は、今日どうにか自力で解けたけど、時間かかった。図形的に考えた（それは、それでいい）のだけど、解説にあるように、数式でシンプルに整理できたほうがよさそう。

\(\{a_i\}\) をあらかじめソートしておくことで i< j のとき \(|a_j - a_i|\ = \ (a_j - a_i)\) にできる。すると、二重Σの内側は、各 i について次のようになる。

\[ \Sigma_{j=i+1}^{N} (a_j - a_i) = \Sigma_{j=i+1}^{N} a_j \ - \ (N-i) a_i \]

これは、累積和をあらかじめ求めておくことで　O(1) で求まる。したがって、全体の計算量ははじめのソートが支配的となり O(N log N): 19855576

コンテスト中に解けなかったもの。もうすこし時間があれば解けたかな…と思ったけど、思っていたより難しかったので、あの方針では解けなかったな。

復習したいポイント：

dp
dfs を K 回前もってしておく

なお、実装時にぽろぽろバグったのが、Ci を番号 i で扱うのと c[i] のとの混乱。

もう一回解いておくべし： 19826224

なんか、いいかげんな貪欲法で WA だしてしまった。反省。

どう工夫しても、最後のひとつの結び目というのができる。隣り合う二本のロープの合計が L 以上のところを選べばよい。ひとつもなければ Impossible となる。ひとつあれば、その結び目を最後に残すように、より左の結び目を左から順に、より右の結び目を右から順にほどき、最後に、選んだひとつをほどく： 19837865

累積和： 19839517

実は、結構バグった。手元で簡単なテストケースをつくってデバッグ。本番でも、落ち着いてできるかな（はじめからバグのないコードが書ければいいのだけど。）

方針はすぐ立ったのだけど、自力で実装しようとした Union Find がバグってたようで、無限に WA の様相だった。まずは、方針があってるかためそうと ACL の dsu を使うようにしたら、あっさり AC: 19842873

Union Find を自分で書くことについては、あとで見直そう。

転倒数（または反転数; inversion number) に関する問題。転倒数は BIT をつかって O(N log N) で求めることができる。

また、毎回のシフトで先頭にあった数が末尾にうつるのだが、その数を ai とすると

数列から ai を取り除くことで、転倒数は ai だけへる（残された数のなかに ai より小さいものが ai 個あるので）
さらに、末尾に ai を付け加えることで、転倒数は (N - (ai + 1)) 個増える

となる。したがって、一度元の数列の転倒数を O(N log N) で求めたあとは、毎回 O(1)：19844750

なお、また int をあふれさせて WA だしてしまった。なにげなく int つかわない！

かけた： 19762015

なかなか AC できなかった。反省： 19765864

桁 dp。とけた： 19766489

とけた： 19767781

なるべく S1 からとるようにしたら、S1 から何文字とることになるか、および、なるべく S2 からとるようにしたら、S2 から何文字とることになるかを求める。それらが両方とも N 以上になれば "YES": 19753167

ABC022C へのリンク

これは、自力で解いておきたかった。ノーヒントで復習したほうがいいので、ここにはヒントになることを書かないでおく： 19753777

これは、どうにか自力でとけた： 19756185

もしかして、また Min-Max? とか思ったけど、そんなわけなかった。解説みて一応提出しておいたけど、間をおいて自力で解いてみよう： 19734017

ちょっとだけ凝った dp という感じ。普通に解けたのだけど、はじめ int をあふれさせてしまって WA。using ll = long long; して用いるようにしよう： 19735515

めぐる式にぶたんで。遠回りが最適になるケースもあるので、上や右にも移動するように bfs にすべき（それで WA だした）： 19736506

各ターンで出現しうる x の値は下のようになる。2x を選ぶと下図における上よりの値、 2x+1 を選ぶとしたよりの値になる。

ここで、N がどこにあるかによって、各プレイヤーのとる戦略が変わる。

もし、\(2^{2k-1} \le N < 2^{2k}\) であれば、Takahashi くんは自分のターンで x が N を超えてしまう危険があるので、Takahashi 君は 2x を、Aoki 君は 2x+1 を選ぶことになる。反対に、 \(2^{2k} \le N < 2^{2k+1}\) であれば、 Takahashi 君は 2x +1 を、Aoki 君は 2x を選ぶ。このとき、どちらが勝つかをシミュレーションすればよい： 19712523

N = 2 で考えてしまった。二回で周期がくるので、任意の K について答えが求まる。 …のだが、これでは K が大きいときに ai が上限を超えてしまう。

そこで諦めたしまったのだが、N=50 で同様に考えればよかった。

はじめ、k=0 のときに {49, 49, 49, ..., 49} とする。

k=1 のときには、一回の操作でこれになればいいので、{99, 48, 48, ..., 48}

k=2 のときには {98, 98, 47, ..., 47}

k=50 で {50, 50, 50, ..., 50}、k=100 で {51,51,51, ..., 51} のようになり、50 回ごとに周期がある。

なので、高々 N-1 回のシミュレーションで答えがもとまる。また、シミュレーションの際に最大値として選ぶ位置は 0, 1, ..., N-1 のように前から選んでいけばよい： 19715575

各列の個数、各行の個数をかぞえておいて、合計が k かつ交差する点に飴ががないか、合計が k+1 でかつ飴がある場合を数え上げればいい。

自分でかいたものは、これをそのまま数えようとして TLE になってしまった。そうではなく、各列、各行の個数の頻度をもっておいて合計が k になる組合せの個数を計算。すると、交差する点に飴があるケースは数えすぎ、合計が k+1 でかつ飴があるケースは数え漏れになるので、N 個の飴すべてについてこれをチェックして足し引きしてやればよい。計算量は O(R+C+N)： 19718154

シミュレーションではなく、考察がいるタイプの問題。まちがえた： 19722676

「\(\{a_i\}\) の平均が A」から「 \(\{a_i - A\}\) の総和が 0 」への読み替えはすぐわかって、総和が 0 になる組み合わせをどうやって数えたものかと。

50 個からの全列挙はできないけど、半分ならギリできそう！というので、つい、「半分全列挙」をしてみたくなって、やってみたものの TLE

dp でしたね。典型的な dp だと思うけど、まだ、ぱっと出てこないなぁ： 19699889

後ろから、なるべく遠くから順位みていく DFS で解けそうだなと実装するも TLE。もしや、C++ で書けば OK かと思い同じものを C++ で書いてみたが同じ。

解説動画にもあるが、実は、この問題は貪欲法でとけるので、到達できる場合には、上記の DFS は一本道にゴールまでたどりつく。したがって、-1 になるケースのみ前もって弾いてやると AC となる。

貪欲でとけることを見抜かずにこれで通すのはどうかとも思うが、 -1 になるのはどういうケースかというのを考えるのは大事だなと思う。（追記：いまの DFS で失敗するケースは、再帰をひとつ上にさかのぼって再トライしても決して成功しないので、そこでアボートさせるしかなかった。…ということを考えると、いまのコードがそのまま貪欲法になるのね。）

解説にあった、後ろからの dp (単調性を用いて工夫）で各ノードからの距離をもとめて答えをだす方法は、あとでもう一度復習したほうがいいと思う： 19703504

ところで、最初の dfs を Haskell で解くときにしらべたのだけど、[Maybe a] から一番はじめの Just a (もしくはなければ Nothing）をもとめるのは msum でよい。firstJust = msum だった。

解けたけど、何回か WA だした。もうすこし慎重に： 19706191

どうやるんだろと思って解説をみてしまったんだけど、普通に Min-Max やれとのこと。 3x3 の〇×くらいだったら、素朴な min-max やれちゃうのか（枝狩りなどはせず）： 19708902

今日から Haskell / C++ の二刀流でいくことにした。いままで Haskell でやったやつの復習を C++ でやればいいかも。

３変数のうち１つを決めたら残り２つは鶴亀算というパターン。

胃袋に上限がないので、食べない日は最後にまとめてよい。その食べない日数をきめたら、最終日に満腹度が 1 以上になるための食べ方は鶴亀算でもとまるので、食べない日数の全探索。

方針はすぐにたったのだけど、実装でなんどもミスってやたら時間がかかってしまった。反省。

a, b, c, d, e と一文字変数名がたくさん使用済なのを、鶴亀算中でも使おうとしたり
最終日にちょうど 0 になってしまったり
なるべく安くすませたいので、安い方でもとめて不足をあとから求めたほうがよかった
途中の引き算結果がマイナスになった計算がおかしくなったり

投稿したもの： 19680450

Imos。各洞くつは、[l, r] の範囲の宝石を点数 s で覆っている。各宝石について、自身を覆っている点数の合計を imos 法で求める。それは、その宝石をとらないことに決めたときに失われる点数に等しい。なので、その最小値を \(\Sigma \ s_i\) から引けばよい： 19683622

以下の方針を思いついたので書いてみる。解説にあったものの１つもこの線だった：

各ノードについて、a からの距離を bfs で求める
求めた距離をつかって、距離 0 から順に dp で到達経路の総数をもとめていく

Haskell で書いたものは WA やら TLE がとれず。おなじものを C++ で書いてみたら、すんなり通って 9ms だった： 19685973

ほかのひとの回答をみるに、最初の dfs のときに dp もやってしまっているものが多いようだった（が、べつに上記のやりかたでも良いよねと思ってる）。

Haskell でも通しておきたいが、あとで。

でかい \({}_nC_r\) を求めるだけ。

Haskell : 19687355
C++ : 19688105

C++ の方は、modinv をソラで書こうとして結構苦労したり。また、階乗や modinv を int で計算してたら桁あふれたりした。

昔の問題で、ふつうの Imos 法。…だが、AC を出してしまった。 Imos が済んでから maximum をとればいいのだけど（それなら AC）、二回サーチするのは無駄なので、サーチしながら max をとるようにしたのだが、 Imos のサーチは添え字 1 から始めるので、最大値の初期値を d[0] にすべきだったという凡ミスでした： 19676692

これは、一度解けなくて解説をみたのを、日をあらためて今日書いてみたというやつ。

x 座標、y 座標それぞれについて dp
s を、'T' で区切られた連続する 'F' の個数（0 以上）の列になおす： [d0, d1, d2, ... ]
d0 は特別扱い（かならず x が増える方向に動く）
x 軸方向の移動に関する xds = [d2, d4, ...] と、y 軸方向の ydx = [d1, d3, ... ] にわける
初期値は dpx[0][d0] と dpy[0][0] がともに True で他は False
xds の 1 つめが d1 だとすると、dpx[1][d0±d1] が True になる

すべて処理したあとに、ターゲット座標にあたる dp 値が x, y ともに True になっているかどうかで判定： 19675494

ACL コンテストでもあるし、みるからに UnionFind かなと思うのだけど、愚直に辺を張ろうとすると多すぎて TLE となる。

まず、x 座標で昇順にソートし、自分より前にあるもの（x 座標が小さい）で、かつ、 y 座標も小さいものの辺を張るようにする（以下のコード片は解説より抜粋）。

ここで、各 i について、[0,(i-1)] の範囲の点をすべてチェックする必要はなく、各連結成分のうち、もっとも y 座標の小さいものを保持しておけばいい。 …というと複雑そうにみえるが、Set をひとつもちいて比較的シンプルに書ける。

当初 S は空
各 yi に対して、
- S に yi より小さいものがなければ（これは S の先頭をみるだけで判定か）yi を S に加える
- S に yi より小さいものがあれば、それらはすべて i と連結する。さらに、そのなかで一番小さいもの以外は S から取り除く（yi はもとから S に追加しない）

投稿例： 19674063

注意：上の投稿例で、最初 loop' の「次」の添え字をしていするために (k+1) を渡してしまってバグってました。

deleteAt k しているので、もともと k+1 の位置にあったものがひとつまえにずれてくるので。

トポロジカルソートの典型的な問題かもしれない。トポロジカルソートしたあと、各ノード v の親は、w → v の辺をもつもののうち最も大きい（より後ろ、根から遠い）ものとなる。

この問題のように、グラフが非循環であることがわかっている場合には、トポロジカルソートは比較的簡単に実装できる。 dfs でも可能だが、今回は入次数０の頂点集合と入次数の配列を更新しながら答えをだしていく方法をとった： 19664161

アフィン変換： 19657798

問題は理解したけど、check 関数をうまくかけず
N が M^2 の形のとき、divisors 関数が M をダブルカウントしてしまって WA

a + b = a `xor` b になる条件もわかったし、 dp[N+1][2] の桁 dp だよなぁと思ったものの、そこから漸化式をうまくつくれなかった。要復習です： 19563074

とけた！解説と同じ解き方かなぁと思ったら（本質的には同じだろうけど）、自分のやった解き方のほうがわかりやすい気がしたので、以下に書いてみる。

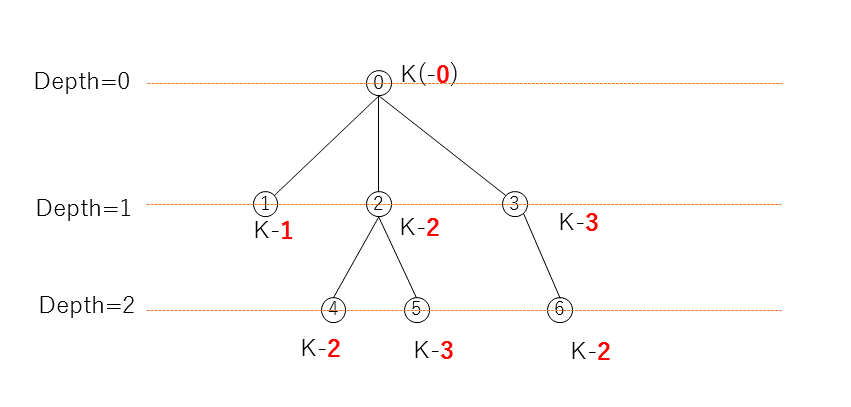
木の根から順に、同じ深さのノードについては一列にならべて左から順に彩色していくことを考える。

根であるノード 0 は、 K 色のうちどの色をつかってもいいので、K 通り
ノード 1 は、ノード 0 がすでに１色つかっているのを避ける必要があるので K - 1 通り
ノード２は、ノード 0, 1 が使っている色を避けて K - 2 通り
...
ノード 5 は、自分より左にあるノード 4 と、親 2 つの色を避けて K - 3 通り

というようになる。各ノードは、位置に応じて K - x 通りの色を使えるのだが、この x (上図で赤字で示した数字）は、以下のように求めることができる。

depth = 0 のとき： 0
depth = 1 のとき（親は１つしかない）：自分より左にあるノードの数＋１
depth ＞ 1 のとき（親が 2 つ以上ある）：自分より左にあるノードの数＋ 2

これを dfs で求めて、最後に k - x_i をすべてかけ合わせればよい： 19546426

ずいぶん簡単だなぁと思って提出して、まんまと WA。

X は \(a_k / 2 \) の奇数倍なので、\(\{a_k / 2\}\) の最小公倍数をもとめて、それの奇数倍がいくつ M 以下の範囲にあるかを数えればよい…。

のだが、その「最小公倍数」自体が、ある \(a_i\) の偶数倍になっていたらだめなわけで。

そんときは 0 個と答えなければならない： 19552246

これ、灰色難易度なんだけど、思いつかなかった。

0 <= x <= y のとき gcd(x, y) == gcd(x, y-x) である（ユークリッドの互除法を思い出そう）ので、操作の過程で gcd は変わらない。カードの数字が全部 a になったときには、gcd (a, a) == a なので、結局もとの数列の gcd を求めればよい： 19555108

昨日とけなかったやつを。解き方は、解説みてもいまいちピンとこなかったのだけど、 f_jhrさんの記事をみたらよくわかった。

ソートも解説のように右端でソートする必然性もなく、この記事と同様に左端でソート。

なお、BIT をつかっても時間制限は厳しく、次の出現位置や答えの蓄積に Map を使っていたらTLE してしまった。使えるところは全て unboxed vector を使うように書き換えてやっと通った： 19528522

自力であっさりとけたよ！

各幼稚園の制御に Set を順序付き多重集合として使い、各幼稚園の最高レートの最小値を求めるのには SegTree を用いた。解説では、後者も順序付き多重集合でやってて、それでもいけたかもしれない： 19529952

とけた。最初、以下の res の前に ! がないものを投稿したら TLE になってしまった。恐ろしい…: 19533686

なにがむずかしいんだろ？って感じで AC。人 N 人と言語 M 個の合計 (N+M) ノードの連結性を考えればいいのだけど、人だけでやろうとするとしんどいらしい： 19536625

なんか文字列の距離を算出するうまい方法をしらなければならないのかな、とか思っちゃった。が、dp でした。

dp[i][j] を、\(\{A_i\}\) が先頭 i 文字のみ\(\{B_i\}\) が先頭 j 文字のみあった場合の答えとする。

i または j が 0 のときの dp[i][j] は簡単に求まる（dp[0][j] = j, dp[i][0] = i）
i, j いずれも 0 でない場合は、\(A_i,\ B_j\) のどちらか片方を消すか、両方のこす場合しかないので、以下の３通りのいずれか（一番小さいもの）
- dp[i-1][j] + 1 : Ai を消した場合
- dp[i][j-1] + 1 : Bj を消した場合
- dp[i-1][j-1] + x, x = {1 (\(A_i\ \ne \ B_j\)), 0 (\(A_i \ = \ \ B_j\))}

回答例： 19518742

ニブタンだなってことはわかったのだけど、判定ルーチンをうまくかけず敗退。

解説をよんだものの、まだ、ピンと来ていない。とりあえず、見よう見まねで書いてみた： 19519951

自分でモノにしたく、再度書いてみた。

bisectLeft を使ううえで、添え字が大きくなるについれて True になる方向の方が扱いやすい。そこで、A0 <= A1 <= ... <= A(n-1) になるよう昇順でソート。

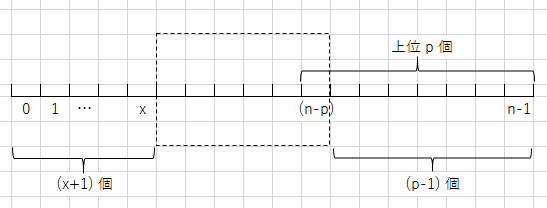
Ax が選択され得るかどうかは、以下のように判定できる。

x >= n-p であれば、もともと p 個以内にはいっているため可能
Ax + M < A(n-p) であれば、不可能
それ以外の場合は、以下の合計が MV 未満であれば不可能（MV 以上であれば可能）
- [0, x] の範囲（x+1 個）については全員が投票しても問題ない
- [n-(p-1), n-1] の範囲 (p-1 個）についても全員が投票しても問題ない
- j <- [x+1, n-p] の範囲については、Ax + M - Aj までなら投票しても問題ない

このように書いたものを再投稿した： 19521339

各色について出現位置の集合をもっておけばいけるかなと思ったのだけど、これだと O(QN log N) で TLE となる。平衡二分木を使おうが、自前で binary search しようがオーダはいっしょだ。

Fenwick Tree または BIT (Binary Indexed Tree) （呼び名が違うだけで同じもの）を使うといいらしい。未修でした。

まず、BIT は snippets/ に用意しておいた： Bit.hs

sum, add ともに計算量は O(logN)。

BIT を使った解放だが、解説のように右端でソートしなくても、左端で考えたほうがわかりやすいのでは？という気がした（参考)

とけた、んだけど、実装にちょっと時間かかりすぎたかも： 19501713

座標圧縮、二次元累積和、そして、全探索といった感じ。すぐに方針は立って解けたのだが、すごく時間がかかってしまった。

最初の版を書くのに少し時間がかかったというのもあるが、その後謎の MLE にでくわす。もしやとおもい、solve の引数の res を !res にしたら、あっさり通った。すこし昔の問題で、メモリ制限がきついというのもあるかもしれないけど、そんなことがあるのか…： 19502534

わからなかったので解説をみた。

下図のように数字をならべる。図中の線はどれも長さが同じで、どの二本をえらんでも一か所で交わる。

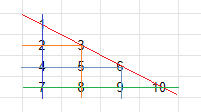
十分大きなグリッドを用意して、上半分を黒、下半分を白で塗る。

上の黒半分の中に、A-1 個の孤立した白いマスをつくっていく。このとき、上半分の黒を分断してしまわないようにする。

下半分にも同様に B-1 個の孤立した黒マスをつくっていく。

たとえば、500 500 の場合はつぎのようになる：

いろいろと要復習。

x 回の移動で玉座にたどりつくことは、\(xK + S \ \equiv \ 0 \ (\textrm{mod}\ N)\) なので、これを解くという問題に帰着できる。

ここまではわかったのだが、解けなかった。

M が素数でないときに、\(A^{(M-2)}\) が mod M における逆元になるとは限らないので、拡張ユークリッドの互除法などを用いる必要がある。

とりあえず見様見真似で提出： 19495399

累積和の各項を剰余で分類するのは、たまに見かける。似てるとこでいうと、ABC164D なども

区間 [l, r) の和が M の倍数であることは、累積和 \(\{B_i\}\) をつくっておいて、 \(B_l \equiv B_r \ (\textrm{mod} M)\) であることと同じ。なので、この問題をとくには、各 \(x \in [0, M)\) について、\(B_i \equiv x \ (\textrm{mod} M)\) となるものの個数をカウントして用いればよい。カウントには、M が大きいので、配列ではなく Map などを用いる： 19451943

コンテストで１時間弱あったので解けるかなぁとか思っていたんだけど、あのままでは解けなかったな。

(1,1) から (h,w) にいたるある一本の経路に着目する。経路中に空白がなければ、その経路は \(3^{(HW-K)}\) 回実現する。

つぎに経路中に空白が k 個ある場合を考える。各空白にはどの文字をいれてもいいわけではなく、その経路がそのマスを横切った方向に応じて、３種類の文字のうちの２つを入れなけらばならない。一方、経路上にない空白（HW-K-k 個ある）には３種類の文字のどれをいれても可。したがって、その経路が実現する回数は \(2^k3^{(HW-K-k)}\) となる。

\[ 2^k3^{(HW-K-k)}\ = \ \frac{2}{3}^k3^{(HW-K)} \]

であることに着目すると、経路上に k 個空白のあるような経路の重みを \(\frac{2}{3}^k\) 倍すればいいので、1 から始めて空白にであうたびに \(\frac{2}{3}\) 倍し、最後に \(3^{(HW-K)}\) を掛ければよいことがわかる。

回答例： 19480433

むずかしく感じなかったのだけど、TLE

連結成分ごとに dfs で数字をわりあてていって、全連結成分についてできれば OK。その通りなのだけど、真面目に連結成分をもとめてリスト化する必要はなくて、全ノードを順番にみていって、未採番なら dfs を回すようにすればよかった： 19437235

xi = 0 に初期化して採番していくと、負の数になることに注意。（連結成分を求めるのをやめたとき、最初、負なら未採番と判定していてバグった）

とけた： 19440021

どうも TLE がとれなくて。BFS は Data.Sequence を queue として使っていたのだけど、どうもこれがあまり速くないようだったので、 unboxed mutable vector をつかった deque を作って通してみた。

テレポート先リストに、距離を付け加えるのが遅いのかなと思って、長さを更新するための特別なエントリを enqueue したり、長さを付け加える push 関数をつくったりした。

長さを更新する特別なエントリをつかう：19449587
後ろにくっつける版：19449574
前にくっつける版：19449559

…が、deque　の完成度が低いので、明日再実装しよう→ した： IOUQueue

サイズを２の冪にしつつ、リングバファにする
メソッド名を一般的なものに合わせる。これとか。
長さがたりないときは grow する。

自力でとけず。Set (平衡二分木）で各アルファベットの出現位置を管理する。平衡二分木は、要素を二分探索できるので、l 以上の出現位置を検索し、それが r 以下なら部分文字列にその文字が出現すると判定できる。もちろん、クエリ１のために要素を追加・削除することも可能： 19423557

問題読み間違えて「？？」ってなってた。これは自力で解いておきたかった： 19425645

とけた。昨日やった第5回ドワンゴからの挑戦状予選Ｂ - Sum AND Subarrays の経験が生きたと思う: 19410282

N <= 40 だと、ビットマスクで前パターンを表現するにはでかすぎるなぁなどと思いつつ（ここで「半分ならいける！」と思い至ればよかった）、方針たてられず敗北。

半分にわければ、消費時間のバリエーションを全列挙できる…ということで、半分全列挙でした： 19410992

すぐに着想はできたのだけど、実装でしくって WA をだした。毎回 \({}_n C_r\) や \(M(M-1)^{(n-1-k)}\) を計算しなおしていては TLE になるので、直前の値をつかって漸進的に求めるようにしたのだが、それでしくじった。

最初のしくじりは、`mod` p をとるべきところで抜かしていたというケアレスミスなんだけど、それを直しても 1 つ WA が残ってしまった。

これは、\(M(M-1)^{(k-1)} = M(M-1)^k / (M-1) \) のように計算していたのだが、 M = 1 のケースでだめだったというもの。なおしたものがこれ： 19412335

こんな微妙な計算をせずに、普通にメモ化的な高速化の方が安全かもしれない（実際、それで最初の AC となった）： 19411964

解けそうな気がしつつ嘘っぱちを Submit してしまった。答えの求め方が結構面白かったこともあり、あとで復習しておきたい。

累積和をつかって、\(N(N-1)/2\) 通りのスコアを計算して、それの降順リストをつくって使うところまでは合っていたのだけど、それの上位 K 個を選んで AND とればいいのではと簡単に考えてしまって WA

より上位にあるビットの方が重要なので、(x | (1 << t)) & Ai == (x | (1 << t)) となる Ai が k 個以上あれば x に (1 << t) を加えるというのを、t <- [40, 39, .. 1] について試していって得られたものが答え： 19386967

単純に Greedy にはいけないし、dp 的なのも難しそう。そこで、解く問題数を固定すれば、その問題数でもっとも合計スコアが高くなる選び方なら Greedy にいけるのではないか。それでニブタンすれば解ける！とか思って書いてみたけど、 WA

たとえば、以下の入力例 (テストケースの b08) は 59 が答えなのだけど、59 問以上解く前提において１問あたりの点数が最も高いのは 200 点問題を37 問解く場合なので、これを選択してしまって間違えた。

正解は、解説にあるとおりなのだけど、たとえば 100 点問題と 200 点問題が十分あるときに（いずれもコンプリートしないときに）、100点問題を 3 問、200点問題を 3 問とく理由はない。なぜなら、200点問題 6 問といたほうが必ず得だから。

そのことから、以下が言える。

１問以上といてかつコンプリートしない配点の問題はたかだか１種類
１問以上といてかつコンプリートしない問題は、コンプリートしないもののなかで最も配点が高いもの。

あとは、コンプリートする問題のバリエーション（2^10通り）すべてについて試せばよい： 19392886

TLE (とケアレスミスの WA) を出してしまったが、その後自力で AC できた。

左端の敵をなるべく右に置いた爆弾で仕留めていくという貪欲法でいいのだが、素朴にやると TLE となる。そこで、現在位置での爆弾の威力と、その爆弾の威力がマイナスになる位置と幅を格納した priority queue を持って、スパースな imos 法のような方法で解いた： 19400089

解説のように、各モンスター i について、巻き添えにできるもっとも右の番号 j を尺取法などで求めておくことでも可。その場合でも、体力の計算に累積和を用いる。

C が比較的小さいので、塗り分けを全通り試せる（30*29*28=24360通り）。各塗分けについて、全グリッドを走査していては間に合わないが、最初に mod グループごとにどの色が何回用いられているかを数えておけば、塗り分けごとの違和感の合計を O(C) で計算できるので間に合う： 19379907

こんどもう一回やろう。

ふつうにとけた： 19381048

これもふつうにとけた： 19382867

グラフの彩色。色をノード、カードの裏表を辺に対応させたグラフにおいて、各辺の端点のうち片方だけ色を塗ることができる（解説では片方だけ「光らせる」）とき、いくつのノードに色を塗れるか。

これは、連結成分ごとにみて、そのサイズを N とすると。それが木なら N-1 個, 木でなければ N 個のノードに色を塗ることができる。

提出例： 19303647

コンテストではそれなりに時間があったのに TLE, WA となって通せず。 DP でとけると気づけば、さほど難しくはなかった。最初、後ろから「もらう dp」で書くのかなと思ったけど、書き始めたら、配る dp で前から書くのが簡単だった。

dp[i] : その町にたどりつくまでに買うことのできる金の最安値

無限大で初期化しておいて、前から順にみて配っていけばいい： 19361665

最小全域木にすれば必ず正しく番号を振れるし、最小全域木はいつもつくれるよな、というのには気づいたものの WA を二連発。

最初は、最小全域木をつくりながら番号を振ろうとして失敗。そんな無理をしなくても、いったんつくってから dfs で確実に番号を振ればよい。のだが、二回目は、よく考えもせずに番号を振ってまた WA。要反省： 19277350

剰余の性質に関する問題。一問も解けずに nosub 不参加となってしまった…。

解説にあるとおり、以下がなりたつため、\(10^N\) の代わりに \(10^N (\textrm{mod} \ M^2) \) をつかって計算できる。

\[ \lfloor \frac{10^N - k M^2}{M} \rfloor \equiv \lfloor \frac{10^N}{M} - k M \rfloor \equiv \lfloor \frac{10^N}{M} \rfloor - k M \equiv \lfloor \frac{10^N}{M} \rfloor (\textrm{mod}\ M) \]

なるほどと思い、それなら \(M^2\) だけでなく \(M^3\) の剰余でもいいはずだよね、と思って試したら、入力例３で答えがあわなかった。どうも、modinv の引数の範囲が Int に収まっていても、途中の計算があふれる場合があるのね。恐ろしいので、modinv の内部計算に Integer を使うように変えておく。

\(M^3\) で計算する必要はないのだが、それで計算したものを submit しておいた： 19295575

とけた： 19258673

なんどか WA だしてしまったけど、いちお自力で AC: 19245823

WA になってしまった理由は、100 までの整数では 5*5*3 パターンしかないねと思ってしまったんだけど（混乱）、100! までなので、25*3, 5*15 はおろか、75 まであった。（素因数分解の添え字のえらびかたのパターン）

まだ記憶にあたらしいので、実力で解いたという感じではないのだけど、ともかく、今回はいっぱつで書けた。

以下のような具体例で dp の更新を考える。 dp[6] は下図のように 4 （通り）。dp[7] を求めるには、まず、この後ろにただ C を付けたケースと、４文字目の C と 7 文字目の C を選んで色を変えたケースを考えれば排他かつ網羅的となり、dp[7] = dp[6] + dp[4]

提出例： 19250522

簡単だった： 19250827

なんか自分の知らないアルゴリズムが必要なのかなと思考停止してしまったが、そうではなかった。以下、解説にあるとおりだけど、ポイントをいくつか。

x が十分ちいさければ、g(x) = x `mod` popcount(x) は素直に実装可能
初回の g(X_i) をどうするかだけが問題

実装例： 19233979

最初 RE を出してしまった。popc - 1 がゼロになってしまうケース。

典型的な dp だと思うんだけど、Bit DP にしたいけど出来ないなぁ（N が大きいのでビット列の状態数が大きくなりすぎる）とか思ってしまった。

とすると、dp は 0 で初期化しておいた上で、

で求まる。それぞれ、すでに k-1 番までで幅 i つかっていて k 番目は貼らなかった場合と、 k-1番目までで幅 i-a だったところから新たに k 番目を貼った場合にあたる 19236667

解説動画をみて実装した。

as の先頭 a を順にとりだし、末尾の数字が a より小さいもののうち最大にバケツを選んで、末尾の数字をaで書き換えていく。バケツを末尾数字で昇順にソートしておけば、バケツの選択は二分探索でき、かつ、書き換えによってソート順は崩れない。なので、単純に「配列」でいいのだけど、長さが前にも後ろにも伸びるので少し工夫がいる： 19211828

解説よんだりしても、あまりピンときてない。いちおう書いてはみたけど、時間をおいて、もういちどよく考えてみよう： 19213605

いま書いたものは、こちらの記事をもとにしている。解説にちかいのは、こちらだと思う。

解説動画を見始めたところで（配る dp の絵をみて）、配る dp + imos 法でいけるじゃないかと書き始めたものの、あわせられず。 dp 配列ひとつで、配る dp と imos の両方をやろうとして混乱していた。解説と同じように、dp 配列と累積和用をわけて AC: 19202626

解説と同じように「もらうdp」でも書いてみたほうがいいかもしれない。

直前に ABC179D をやっていたので、これは自力で AC。累積和ともらう dp といった感じで： 19203562

今日から水色埋め。2AC/day ペースで二月末くらいをめどに。

木構造に対する imos 法のようなやつかなと思ったんだけど、コンテスト中には解けなかった。

その見立ては正しくて、自分と自分より葉に近いノードに加える数値を記録しておいて、最後に足しこんでいけばいいのだが、少し難しいのは、逆のケース。自分より「下」以外に足すケース。これは、全体に足したうえで、自分より葉に近いノードからは同じだけ引けばいい。

各辺の両端を記憶しておく (as, bs)
dfs のため、各ノードからいけるノードのリストをつくっておく (es)
1つもの dfs で各ノードの深さ（根=node 0 からの距離）を測っておく
各クエリについて、
- 足す側が根に近ければ根に +x (全体に x 足すのに相当) し、一つ「下」のノードに -x
- 足す側が葉に近ければ、そこに +x
２つめの dfs で累積和（ここでも各ノードの深さを用いる）

実装例： 19176602

行列の要素はすべて異なるので、同じ行があったらどうしようという心配は無用だった。あと、直接交換可能でなくとも、交換可能なもの同士のグラフで同じ連結成分にあるもの同士は交換可能。なので、解説にあるとおり、連結成分ごとにそのサイズの階乗を掛けていけばよい。列の交換と行の交換は独立に考えられるので、それぞれの積をさらにかけたものが答え： 19189642

「平均値最大化」という手法が身についていなくて解けなかったのと、答えが Double になる場合の二分探索でもまごついた。

条件：濃度が x 以上になるように k 個選べるかどうか

この条件を満たすかどうかは、

\[ \frac{\Sigma w_i p_i}{\Sigma w_i} \ge x \]

と表せる。この式を変形すると、

\[ \Sigma w_i (p_i - x) \ge 0 \]

となり、これなら \(w_i (p_i - x)\)を大きいものから k 個足した結果が 0 以上かどうかで判定可能。

なお、浮動小数点数での二分探索については、前回解いたときには専用のものをその場で書いたのだけど、今回のように bisect を使った方が見通しは良いように思う。

「a[0], ..., a[n-1] の平均が K 以上」を「a[0]-K, ..., a[n-1]-K の総和が 0 以上」にするテクは二分探索に限らずちょくちょく見るらしいので要注意。

典型的な巡回セールスマン問題。いちど蟻本みて書いたのだけど、今回もみて書いた。

S をすでに巡回済の頂点の集合としたとき、現在 v にいる状態から、残りすべての頂点をめぐって頂点0に到達するときの移動コストの最小値を dp[S][v] とあらわす。すると、初期値および漸化式は以下のようになる。