![]() を
を ![]() 上の有限次元ベクトル空間、
上の有限次元ベクトル空間、
![]() をその部分空間とし、かつ
をその部分空間とし、かつ ![]() とする。
とする。
![]() を
を ![]() の基底とし、かつ
の基底とし、かつ ![]() に属さない元
に属さない元 ![]() を取る。このとき
を取る。このとき ![]() は一次独立である。このことを証明せよ。
は一次独立である。このことを証明せよ。
![]() が一次従属であると仮定すると、
全てが 0 ではないスカラーの列
が一次従属であると仮定すると、
全てが 0 ではないスカラーの列 ![]() が存在し、
次の式を満たす。
が存在し、
次の式を満たす。
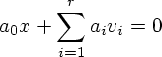
ここでもし ![]() だとすると
だとすると ![]() となってしまい、
となってしまい、
![]() が
が ![]() の基底である(したがって一次独立である)
ことに反するため、
の基底である(したがって一次独立である)
ことに反するため、![]() である。そこで、上式を
である。そこで、上式を ![]() で割って整理すると、
で割って整理すると、
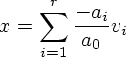
となる。![]() が
が ![]() の基底ベクトルの線形結合で表現されることは
の基底ベクトルの線形結合で表現されることは
![]() を意味し、条件に反する。
を意味し、条件に反する。
よって、![]() は一次独立である。
は一次独立である。
2008-01-24: Web で公開されている 「解答と講評」には具体的な解答例が示されていなかったため、 自分で書いてみた。これで大丈夫じゃないかとは思うんだけど……。